Fala, meus consagrados! Tudo beleza com vocês?
Vamos entender o que é e como criar funções recursivas.
Teoria
A recursão é quando um módulo faz uma chamada ou ativa a si mesmo. É bem exemplificada quando um módulo é definido em termos de si mesmo.
Uma grande vantagem sua é que um conjunto infinito de sentenças possíveis pode ser definido, analisado ou produzido por um programa finito de computador.
Pontos positivos:
- Um programa recursivo:
- É mais elegante e menor que a sua versão iterativa; e
- Exibe com maior clareza o processo utilizado;
- Desde que o problema ou os dados sejam naturalmente definidos através de recorrência;
Pontos negativos:
- Um programa recursivo:
- Exige mais espaço de memória; e
- É mais lento do que a versão iterativa na grande maioria dos casos.
Como forma de comparação, veremos dois códigos para calcular o fatorial de um número: um código iterativo e outro recursivo.
Exemplo do código iterativo:
Algoritmo fatorialIterativo;
var resultado, num: inteiro;
função fatorial(n: inteiro): inteiro
var aux, fat: inteiro;
início da função
aux := 1;
fat := 1;
enquanto (aux <= n) faça
fat := fat * aux;
aux := aux + 1;
fim do enquanto
retorne(fat);
fim da função
início
leia(num);
resultado := fatorial(num);
escreva(“Fatorial iterativo: ”, resultado);
fim
Fazendo o teste chinês para a variável num igual a 5, temos a seguinte tabela:
|
num |
resultado |
n |
aux |
fat |
|
5 |
– |
– |
– |
– |
|
5 |
– |
5 |
1 |
1 |
|
5 |
– |
5 |
2 |
1 |
|
5 |
– |
5 |
3 |
2 |
|
5 |
– |
5 |
4 |
6 |
|
5 |
– |
5 |
5 |
24 |
|
5 |
– |
5 |
6 |
120 |
|
5 |
120 |
– |
– |
– |
Agora veremos a versão da função fatorial, agora de forma recursiva:
Algoritmo fatorialRecursivo;
var resultado, num: inteiro;
função fatorial(n: inteiro): inteiro
início da função
se (n <= 1) então
retorne(1);
senão
retorne(n * fatorial(n – 1));
fim do se
fim da função
início
leia(num);
resultado := fatorial(num);
escreva(“Fatorial recursivo: ”, resultado);
fim
Fazendo o teste chinês para a variável num igual a 5, temos a seguinte tabela:
|
num |
resultado |
n |
Ida |
Retorna |
|
|
5 |
– |
– |
– |
– |
– |
|
5 |
– |
5 |
5 * fatorial(4) |
5 * 24 |
120 |
|
5 |
– |
4 |
4 * fatorial(3) |
4 * 6 |
24 |
|
5 |
– |
3 |
3 * fatorial(2) |
3 * 2 |
6 |
|
5 |
– |
2 |
2 * fatorial(1) |
2 * 1 |
2 |
|
5 |
– |
1 |
1 |
1 |
1 |
|
5 |
120 |
– |
– |
– |
– |
Percebam a quantidade menor de linhas de código e um código mais enxuto da versão recursiva em relação à sua versão iterativa.
Quando trabalhamos com código recursivo, temos que entender que haverá a criação de uma pilha de operações, pois a função vai se chamando até chegar a um valor de retorno, que no caso acima é quando o valor do parâmetro n for menor que ou igual a 1 (se (n <= 1) então retorne(1)).
Quando se chega ao valor definido para retorno, as operações empilhadas vão sendo feitas e retornadas, como está nas colunas de retorno da tabela do teste chinês.
Na figura 1, temos o esquema visual da pilha de operações recursivas.
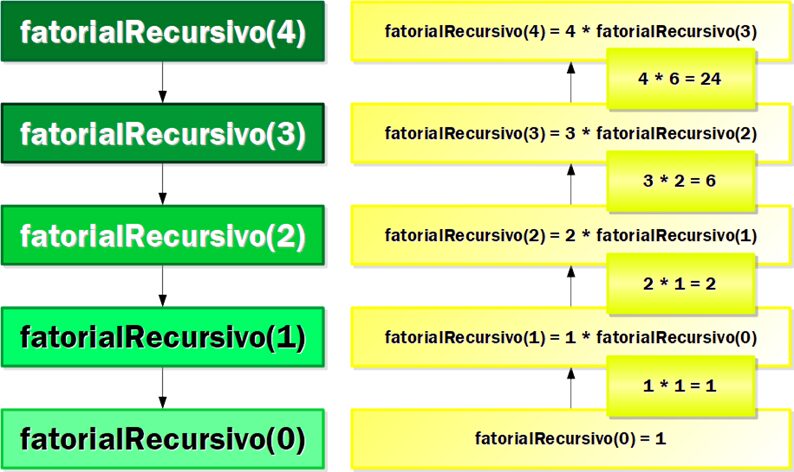
Figura 1: pilha de operações recursivas.
Finalmente, temos dois tipos de códigos recursivos:
- Diretamente recursivo:
- Quando o módulo P contiver uma referência explícita a si próprio;
- Indiretamente recursivo:
- Quando o módulo P contiver uma referência a outro módulo Q;
- Que por sua vez contém uma referência direta ou indireta a P.
- Quando o módulo P contiver uma referência a outro módulo Q;
Questões de concursos
[Quadrix 2019 Prefeitura de Jataí/GO – Analista de Tecnologia da Informação] A situação em que dois subprogramas fazem chamadas recíprocas, como, por exemplo, um subprograma P faz uma chamada a um subprograma J, que, por sua vez, faz uma chamada a P, é caracterizada como uma
[A] recursividade direta.
[B] recursividade indireta.
[C] recursividade simples.
[D] lista linear simples.
[E] lista circular
Comentários:
O enunciado traz a descrição do código indiretamente recursivo.
Gabarito: letra B.
[Instituto AOCP 2020 Prefeitura de Novo Hamburgo/RS – Analista de Desenvolvimento de Sistemas] Analise o seguinte algoritmo em pseudo-código e assinale a alternativa correta.

[A] A primeira chamada da “funcao_A” com o argumento 2 provoca uma segunda chamada da “funcao_A” com o argumento 1.
[B] Como o programa é iterativo, faz-se necessário mais uma variável além de “f”, por exemplo, para armazenar os diversos passos do processamento.
[C] Quando a “funcao_A” é chamada com um argumento de 1, a função retorna o argumento 0 e não necessita executar a iteração.
[D] O algoritmo retorna erro para quando o argumento passado possui um valor maior que 1000 e menor que o valor máximo de um número inteiro.
[E] Há um laço que é executado de 1 a n, multiplicando progressivamente cada número pelo produto móvel dado por “f = funcao_A(n-1)*n;”.
Comentários:
Comentando cada letra, temos:
- Letra A: CERTO. A primeira chamada da “funcao_A” com o argumento 2 provoca uma segunda chamada da “funcao_A” com o argumento 1 (n – 1);
- Letra B: ERRADO. O código não é iterativo e sim recursivo. Há uma chamada da função dentro dela;
- Letra C: ERRADO. O texto correto é: quando a “funcao_A” é chamada com um argumento de 0 ou 1, a função retorna o valor 1;
- Letra D: ERRADO. O algoritmo não retorna erro para quando o argumento passado possui um valor maior que 1000 e menor que o valor máximo de um número inteiro;
- Letra E: ERRADO. Não existe uma estrutura de repetição para termos laço dentro da função recursiva da questão.
Gabarito: letra A.
Então é isso!
[]s e até a próxima!
_________________________
Professor Rogerão Araújo
![[Preparatórios] Concursos TI – Cabeçalho](https://blog-static.infra.grancursosonline.com.br/wp-content/uploads/2026/01/11153738/ti-10off-cabecalho.webp)

![[Preparatórios] Concursos TI – Post](https://blog-static.infra.grancursosonline.com.br/wp-content/uploads/2026/01/11153733/ti-10off-post.webp)