Questões de PA e questões de PG são assuntos muito cobradas especialmente em carreiras policiais, militares e administrativas. Além disso, se você vai prestar concurso para qualquer área de matemática, também vai encontrá-las no cronograma. A matemática é, afinal de contas, uma das principais matérias de conhecimentos básicos a cair em concurso públicos. Mas o que são a PA E PG? E como estudar questões de PA e questões de PG para concursos públicos? Nós te contamos!
Questões de PA e questões de PG para concursos públicos: conceitos
O conceito básico tanto da PA quanto da PG, é que são progressões de números. Isto é, uma coleção numérica que segue uma determinada ordem. Quando apresentadas em questões, essas progressões numéricas podem ser classificadas como finitas ou infinitas e sempre estão entre parênteses. Observe:
- (60,50,40,30,20,10) – É uma progressão numérica (aritmética) finita, pois nós conhecemos o último termo.
- (45, 15, 5, …) – É uma progressão numérica (geométrica) infinita, pois não conhecemos o último termo. Ao invés disso, temos a presença dos três pontos […].
Mas como identificar se estamos falando de um questão de PA (Progressão Aritmética) ou uma questão de PG(Progressão Geométrica) em concursos públicos? Isso vai depender da análise da razão (r).
Razão (r) de PA Ou PG
De modo resumido, podemos identificar a razão de progressões numéricas como a regra principal para a mudança e progressão dos termos. A maneira como calculamos a razão da PA e da PG são diferentes. Confira as principais fórmulas para cada caso:
Fórmula de razão da PA:

Fórmula para questões de PA – razão
Fórmula de razão da PG:
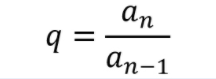
Fórmula para questões de PG – razão
Muitas questões de concurso público podem estar baseadas justamente em calcular ou avaliar essa razão. Confira um exemplo abaixo:
(2011. CESPE CEBRASPE – BRB – Escriturário)
Considerando que, em uma progressão aritmética de termos a1, a2, …, an, …, a razão seja positiva, a1 = 2 e os termos a1, a3 e a11 estejam, nessa ordem, em progressão geométrica, julgue os itens a seguir.
A razão dessa progressão aritmética será um número racional, não inteiro.
Resposta comentada
Item Errado.
Como vimos, a razão da progressão aritmética é igual a 3. Portanto, é um número inteiro.
Para a progressão aritmética, podemos escrever:

Agora, queremos que a1, a3 e a11 estejam em progressão geométrica. Para isso, devemos ter uma razão q, de modo que:

Chegamos a uma igualdade envolvendo a razão da PG. Agora, podemos resolver o problema:
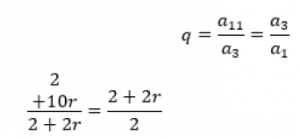
Usando as propriedades de razão e proporção, podemos subtrair o denominador do numerador.
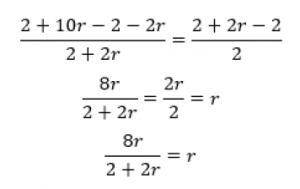
Como a razão é positiva, temos que ela não pode ser zero. Por isso, podemos cortar o r de ambos os lados.

Para n ímpar, o número n-1 será par, portanto 3(n-1) também será par. O termo ímpar será a soma de 2 com outro número par, logo todos os termos a1, a3, a5 etc. são pares.
*Resposta pelo professor Thiago Fernando Cardoso da Silva da equipe Gran Cursos Questões
Questões de PA e questões de PG para concursos públicos: como são cobradas?
As questões de PA e questões de PG para concursos públicos geralmente transitam com mais frequência em torno da identificação de termos gerais ou somas de termos específicos da progressão. Veja abaixo alguns exemplos de questões comentadas!
Questões de PG para concursos públicos – Soma de termos de uma PG infinita
(2019. EEAR – Sargento)
Dada a equação 20x + 10x + 5x + … = 5, em que o primeiro membro representa a soma dos termos de uma progressão geométrica infinita, o valor de 1/x é
(A). 12
(B). 10
(C). 8
(D). 5
Resposta comentada
Item C.
– Considerando que, na PG, A1= 20x, a razão q= 1/2 e Sn= 5;
– Assim, como Sn= A1/ (1-q), que 5= 20.x/ (1-1/2), então x= 1/8;
– Dessa forma, se x= 1/8, então 1/x= 8 .
*-Resposta pelo professor João Carlos de Freitas da equipe Gran Cursos Questões.
Questões de PA para concursos públicos – Identificação de termos
(2020. ESA – Técnico em Enfermagem – 1º Simulado Pós-edital )
Preparando-se para uma maratona aquática importante, com percurso de 10 km, certo sargento treina diariamente e, a cada dia, nada 100 m a mais do que no dia anterior. Mantendo este ritmo, no décimo dia, ele nadou um total de 2.500 m.
Desta forma, pode-se estimar que, para estar em condições de cumprir essa prova, esse marinheiro deverá treinar, no mínimo, durante:
(A). 75 dias.
(B). 85 dias.
(C). 95 dias.
(D). 105 dias.
(E). 115 dias.
Clique aqui para se cadastrar GRATUITAMENTE hoje mesmo e revolucione seus estudos!
Quer ficar por dentro dos concursos públicos abertos e previstos pelo Brasil?
Clique nos links abaixo:
Receba gratuitamente no seu celular as principais notícias do mundo dos concursos!
Clique no link abaixo e inscreva-se gratuitamente:
![[JANELA DE OURO] R$ 54,90 – Cabeçalho](https://blog-static.infra.grancursosonline.com.br/wp-content/uploads/2026/02/09091020/janela-ouro-preco-promo-cabecalho.webp)

![[JANELA DE OURO] R$ 54,90 – Post](https://blog-static.infra.grancursosonline.com.br/wp-content/uploads/2026/02/09091401/janela-ouro-preco-promo-post.webp)







Participe da conversa