Regressão Linear em Aprendizado de Máquina

Bem-vindos ao mundo da regressão linear no contexto de machine learning! Se você está se preparando para concursos públicos na área de tecnologia, é fundamental entender os conceitos por trás desse importante algoritmo. Mas não se preocupe, estamos aqui para tornar tudo mais fácil de aprender!

A regressão linear é uma técnica de aprendizado de máquina que busca estabelecer uma relação linear entre uma variável de saída (variável dependente) e uma ou mais variáveis de entrada (variáveis independentes). Ela é amplamente utilizada para prever valores contínuos com base em dados históricos. Por exemplo, você pode usar regressão linear para prever o preço de uma casa com base em características como tamanho, número de quartos, localização etc.

A ideia por trás da regressão linear é encontrar a linha reta que melhor se ajusta aos dados, minimizando a diferença entre os valores preditos pela linha e os valores reais. Essa linha é determinada por dois parâmetros: a inclinação (coeficiente angular) e a intercepção (coeficiente linear).

A figura a seguir mostra um exemplo de uma regressão linear entre as variáveis idade e pressão arterial:

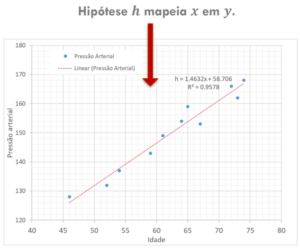
Quando se trata de concursos públicos, é importante estar familiarizado com os principais conceitos da regressão linear. Você pode ser perguntado sobre os diferentes tipos de regressão, como regressão linear simples e regressão linear múltipla. A regressão linear simples envolve apenas uma variável independente, enquanto a regressão linear múltipla considera várias variáveis independentes para fazer as previsões.

Outro aspecto importante da regressão linear é a avaliação do desempenho do modelo. Você pode encontrar perguntas sobre medidas de erro, como o erro quadrático médio (MSE) e o coeficiente de determinação (R²), que medem a precisão das previsões feitas pelo modelo.

O Erro Quadrático Médio é uma medida que calcula a média dos quadrados das diferenças entre os valores preditos pelo modelo e os valores reais do conjunto de dados. Ele fornece uma estimativa de quão próximo os valores preditos estão dos valores reais. Quanto menor o MSE, melhor o desempenho do modelo, pois indica que as previsões estão mais próximas dos valores reais. O MSE é calculado somando-se os quadrados dos resíduos (diferenças) entre os valores preditos e os valores reais e dividindo pelo número total de amostras.

Já o Coeficiente de Determinação (R²) mede a proporção da variabilidade da variável dependente que é explicada pelo modelo. Ele varia entre 0 e 1, onde um valor de 1 indica que o modelo é capaz de explicar perfeitamente a variabilidade dos dados, e um valor próximo de 0 indica que o modelo não é capaz de explicar a variabilidade em absoluto. O R² é calculado como a proporção da soma dos quadrados dos resíduos em relação à soma total dos quadrados, sendo quanto mais próximo de 1, melhor o ajuste do modelo aos dados.

O MSE e o R² estão relacionados. Enquanto o MSE nos dá uma medida absoluta do erro médio do modelo, o R² nos dá uma medida relativa de quão bem o modelo se ajusta aos dados em comparação com um modelo de referência simples (geralmente uma linha reta horizontal representando a média dos valores de saída).

Continuando os estudos, é essencial entender que a regressão linear tem suas limitações. Ela assume uma relação linear entre as variáveis, o que pode não ser válido em todos os casos. Além disso, a regressão linear é sensível a valores atípicos e pode não ser adequada para problemas complexos com relações não lineares.

Felizmente, existem variações e extensões da regressão linear, como a regressão linear regularizada (Ridge e Lasso), que ajudam a superar algumas dessas limitações. Essas técnicas incorporam termos de regularização para controlar a complexidade do modelo e evitar o sobreajuste.

A regularização é uma técnica usada para lidar com o sobreajuste (overfitting) em modelos de regressão, evitando que eles sejam excessivamente complexos e sensíveis aos dados de treinamento. Ela adiciona um termo de regularização à função de perda do modelo, o qual penaliza os coeficientes que têm grandes valores, reduzindo sua influência no resultado final.

Existem duas técnicas de regularização amplamente utilizadas em regressão: Ridge e Lasso.

A regularização Ridge, também conhecida como Regressão Ridge, adiciona um termo de penalidade L2 à função de perda. Esse termo é proporcional à soma dos quadrados dos coeficientes do modelo. O efeito da regularização Ridge é diminuir os valores dos coeficientes, mas sem torná-los exatamente zero. Isso ajuda a reduzir a complexidade do modelo e a controlar a magnitude dos coeficientes.

Por outro lado, a regularização Lasso, também conhecida como Regressão Lasso, adiciona um termo de penalidade L1 à função de perda. Esse termo é proporcional à soma dos valores absolutos dos coeficientes. A regularização Lasso tem a capacidade de reduzir os coeficientes para zero, o que permite a seleção automática de recursos. Isso significa que a regressão Lasso pode ser usada como uma técnica de seleção de recursos, mantendo apenas os coeficientes mais importantes e descartando os menos relevantes.

Tanto a regularização Ridge quanto a Lasso possuem um parâmetro de regularização, chamado de lambda (λ) ou alpha (α), que controla a força da penalidade aplicada aos coeficientes. Valores maiores de lambda ou alpha resultam em uma maior regularização, levando a coeficientes mais próximos de zero.

A regressão linear é um dos fundamentos essenciais do machine learning e pode ser uma base sólida para construir conhecimento adicional sobre algoritmos mais complexos. Portanto, estude, pratique e esteja pronto para brilhar nos concursos públicos em tecnologia! Vamos praticar:

Ano: 2013 Banca: Quadrix Órgão: DATAPREV

Assinale a alternativa que contém uma justificativa para a utilização de um modelo de regressão linear múltipla em substituição a um modelo de regressão linear simples para a análise de dados.

A Quando existe um número excessivo de dados a serem analisados.

B Quando o resíduo é muito grande.

C Quando a regressão é ausente.

D Quando se necessita de mais de uma variável independente no modelo de regressão.

E Quando a regressão é fracamente positiva.

Gabarito: D

Comentários: Como falado no texto, a regressão linear múltipla recebe mais de uma variável independente como entrada e apresenta uma variável dependente (y) como saída. As demais alternativas são devaneios do examinador.

Prova: FUNDATEC – 2022 – AGERGS – Técnico Superior Engenheiro de Dados

Para minimizar o erro de estimação de um valor contínuo baseado em um conjunto de atributos, o algoritmo mais adequado para o problema é:

A AGNES – Aglomerative Nesting.

B Naïve Bayes.

C Árvore de sinergia.

D Regressão linear.

E K-means.

Gabarito: D

Comentários: A questão apresenta uma situação em que o objetivo é minimizar o erro de estimação de um valor contínuo com base em um conjunto de atributos. Vamos analisar cada alternativa e identificar a mais adequada para resolver o problema:

1. A) AGNES – Aglomerative Nesting: O algoritmo AGNES é utilizado para realizar a análise de agrupamento hierárquico, não sendo específico para problemas de regressão.
2. B) Naïve Bayes: O algoritmo Naïve Bayes é amplamente utilizado para classificação de dados com base em probabilidades condicionais. Embora seja útil para problemas de classificação, não é o mais adequado para problemas de regressão.
3. C) Árvore de sinergia: A opção “Árvore de sinergia” não é um algoritmo comumente utilizado em problemas de regressão. Portanto, não é a alternativa mais adequada.
4. D) Regressão linear: A regressão linear é um algoritmo amplamente utilizado para problemas de estimação de valores contínuos. É especialmente adequada quando há uma relação linear entre os atributos e a variável de destino. Portanto, a alternativa D é a mais apropriada para minimizar o erro de estimação nesse contexto.
5. E) K-means: O algoritmo K-means é uma técnica de agrupamento usada para separar dados em grupos, não sendo a melhor escolha para problemas de regressão.

Dessa forma, a resposta correta para a questão é a alternativa D) Regressão linear. Esse algoritmo é projetado especificamente para minimizar o erro de estimação em problemas de regressão, tornando-se a escolha mais adequada para o problema apresentado.